2021. 7. 20. 14:07ㆍpython
난이도 ●◐○ l 풀이 시간 20분 l 시간 제한 1초 l 메모리 제한 128MB l
문제
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다. 태일이는 이 얇은 바닥을 1 x 2의 덮개, 2 x 1의 덮개, 2 x 2의 덮개를 이용해 채우고자 한다.

이때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오. 예를 들어 2 x 3 크기의 바닥을 채우는 경우의 수는 5가지이다.
입력조건
첫째 줄에 N이 주어진다. ( 1 <= N <= 1,000 )
출력조건
첫째 줄에 2 x N 크기의 바닥을 채우는 방법의 수를 796,796 으로 나눈 나머지를 출력한다.
문제해설
이 문제 또한 마찬가지로 다아나믹 프로그래밍의 기초예제에서 빠질 수 없는 타일링 문제 유형이다. 다아나믹 프로그래밍 문제에서는 종종 결과를 어떤 수로 나눈 결과를 출력하라는 내용이 들어가 있는 경우가 많다. 이 문제에서도 796,796으로 나눈 나머지를 출력하라고 하는데, 이는 단지 결과값이 굉장히 커질 수 있기 때문에 그런 것이다. 따라서 값을 계산할 때마다 특정한 수로 나눈 나머지만 취하도록 하면 된다.이 문제 또한 그림으로 그려서 생각하면 어렵지 않게 풀 수 있다. 예를 들어 N이 3일 때 바닥을 덮개로 채울 수 있는 모든 경우의 수는 다음과 같다.


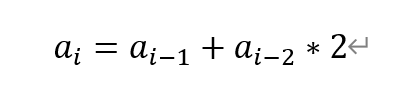

답안예시
# 정수 N을 입력받기
n = int(input())
# 앞서 계산된 결과를 저장하기 위한 DP테이블 초기화
d = [0] * 1001
# 다이나믹 프로그래밍(Dynamic Programming) 진행 (보텀업)
d[1] = 1
d[3] = 3
for i in range(3, n + 1):
d[i] = (d[i - 1] + 2 * d[i - 2] % 796796
# 계산된 결과 출력
print(d[n])
본 포스팅은 ‘이것이 코딩 테스트다 with 파이썬’을 읽고 공부한 내용을 바탕으로 작성하였습니다.
작성자 : 엄코딩 eomcoding
'python' 카테고리의 다른 글
| Python 86 - 다이나믹 프로그래밍 실전문제4 ("효율적인 화폐 구성") (0) | 2021.07.23 |
|---|---|
| Python 84 - 다이나믹 프로그래밍 실전문제2 ("개미 전사") (0) | 2021.07.19 |
| Python 83 - 다이나믹 프로그래밍 실전문제1 ("1로 만들기") (0) | 2021.07.18 |
| Python 82 - 다이나믹 프로그래밍 (0) | 2021.07.17 |
| Python 81 - 이진탐색 실전문제 2("떡볶이 떡 만들기") (0) | 2021.07.16 |