2021. 7. 4. 15:33ㆍpython
계수 정렬
계수 정렬(Count Sort) 알고리즘은 특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠른 정렬 알고리즘이다. 모든 데이터가 양의 정수인 상황을 가정해보자. 데이터의 개수가 N, 데이터 중 최대값이 K일 때, 계수 정렬은 최악의 경우에도 수행 시간 O(N+K)를 보장한다. 계수 정렬은 이처럼 매우 빠르게 동작할 뿐만 아니라 원리 또한 매우 간단하다. 다만, 계수 정렬은 '데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때' 만 사용할 수 있다. 예를 들어 데이터의 값이 무한한 범위를 가질 수 있는 실수형 데이터가 주어지는 경우 계수 정렬은 사용하기 어렵다. 일반적으로 가장 큰 데이터와 가장 작은 데이터의 차이가 1,000,000을 넘지 않을 때 효과적으로 사용할 수 있다.
예를 들어 0 이상 100 이하인 성적 데이터를 정렬할 떄 계수 정렬이 효과적이다. 다만, 가장 큰 데이터와 가장 작은 데이터의 차이가 너무 크다면 계수 정렬은 사용할 수 없다. 계수 정렬이 이러한 특징을 가지는 이유는, 계수 정렬을 이용할 떄 는 '모든 범위를 담을 수 있는 크기의 리스트(배열)를 선언' 해야하기 때문이다. 예를 들어 가장 큰 데이터와 가장 작은 데이터의 차이가 1,000,000이라면 총 1,000,001 개의 데이터가 들어갈 수 있는 리스트를 초기화해야한다. 여기서 1개를 더해주는 이유는 0 부터 1,000,000까지는 총 1,000,001 개의 수가 존재하기 때문이다.
계수 정렬은 앞서 다루었던 3가지 정렬 알고리즘 처럼 직접 데이터의 값을 비교한 뒤에 위치를 변경하며 정렬하는 방식( 비교 기반의 정렬 알고리즘)이 아니다.
계수 정렬은 일반적으로 별도의 리스트를 선언하고 그 안에 정렬에 대한 정보를 담는다는 특징이 있다. 구체적인 예시를 통해 계수 정렬에 대해서 이해해보자. 단, 말했듯이 계수 정렬은 데이터의 크기가 제한 되어 있을 때에 한해서 데이터의 개수가 매우 많더라도 빠르게 동작한다. 따라서 예시 또한 앞서 다루었던 예시와 다르게 많은 데이터가 존재하는 경우를 살펴보자.
- 초기단계 : 7 5 9 0 3 1 6 2 9 1 4 8 0 5 2
계수 정렬은, 먼저 가장 큰 데이터와 가장 작은 데이터의 범위가 모두 담길 수 있도록 하나의 리스트를 생성한다. 현재 예시에서는 가장 큰 데이터가 '9' 이고 가장 작은 데이터가 '0' 이다. 따라서 우리가 정렬할 데이터의 범위는 0부터 9까지이므로 리스트의 인덱스가 모든 범위를 포함할 수 있도록 한다. 다시 말해 우리는 단순히 크기가 10인 리스트를 선언하면 된다. 처음에는 리스트의 모든 데이터가 0이 되도록 초기화한다.
그다음 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가시키면 계수정렬이 완료된다. 직접 확인해보자.

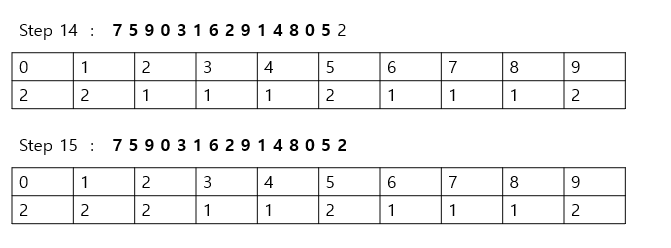
결과적으로 위와 같이 리스트에는 각 데이터가 몇 번 등장했는지 그 횟수가 기록된다. 예를 들어 5인 인덱스의 값이 2이므로 '5'는 2번 등장한 것이다. 이 리스트에 저장된 데이터 자체가 정렬된 형태 그 자체라고 할 수 있다. 정렬된 결과를 직접 눈으로 확인하고 싶다면, 리스트의 첫 번째 데이터부터 하나씩 그 값만큼 인덱스를 출력하면 된다. 예를 들면 '0' 인덱스의 값이 2이므로 0을 2번 출력하면 된다.

결과적으로 최종 정렬된 결과인 '0 0 1 1 2 2 3 4 5 5 6 7 8 9 9' 가 출력되는 것을 알 수 있다.
이를 소스코드로 표현하면 다음과 같다.
계수 정렬 소스코드
# 모든 원소의 값이 0보다 크거나 같다고 가정
array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
# 모든 범위를 포함하는 리스트 선언( 모든 값은 0 으로 초기화)
count = [0] * (max(array) + 1)
for i in range(len(array)):
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
for j in range(count[i]):
print(i, end=' ') # 띄어쓰기 구분으로 등장한 횟수 만큼 인덱스 출력
출력결과
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9 계수 정렬의 시간 복잡도
앞서 언급했듯이 모든 데이터가 양의 정수인 상황에서 데이터의 개수를 N, 데이터 중 최댓값의 크기를 K라고 할 떄, 계수 정렬의 시간 복잡도는 O(N + K)이다. 계수정렬은 앞에서부터 데이터를 하나씩 확인하면서 리스트에서 적절한 인덱스의 값을 1씩 증가시킬 뿐만 아니라, 추후에 리스트의 각 인덱스에 해당하는 값들을 확인할 때 데이터 중 최댓값의 크기만큼 반복을 수행해야 하기 때문이다. 따라서 데이터의 범위만 한정되어 있다면 효과적으로 사용할 수 있으며 항상 빠르게 동작한다. 사실상 현존하는 정렬 알고리즘 중에서 기수 정렬(Radix Sort)과 더불어 가장 빠르다고 볼 수 있다.
보통 기수 정렬은 계수 정렬에 비해서 동작은 느리지만, 처리할 수 있는 정수의 크기는 더 크다. 다만 알고리즘 원리나 소스코드는 더 복잡하다. 다행히 반드시 기수 정렬을 이용해야만 해결할 수 있는 문제는 코딩테스트에서 거의 출제되지 않으므로, 책에서는 기수 정렬에 대해서 자세히 다루지는 않는다.
계수 정렬의 공간 복잡도
계수 정렬은 때에 따라서 심각한 비효율성을 초래할 수도 있다. 예를 들어서 데이터가 0 과 999,999 단 2개만 존재한다고 가정해보자. 이럴 때에도 리스트의 크기가 100만 개가 되도록 선언해야 한다. 따라서 항상 사용할 수 있는 정렬 알고리즘은 아니며, 동일한 값을 가지는 데이터가 여러 개 등장할 때 적합하다. 예를 들어 성적의 경우 100점을 맞은 학생이 어러명 일수 있기 떄문에 계수 정렬이 효과적이다. 반면에 앞서 설명한 퀵 정렬은 일반적인 경우에서 평균적으로 빠르게 동작하기 떄문에 데이터의 특성을 파악하기 어렵다면 퀵 정렬을 이용하는 것이 유리하다.
다시 말해 계수 정렬은 데이터의 크기가 한정되어 있고, 데이터의 크기가 많이 중복되어 있을 수록 유리하며 항상 사용할 수는 없다. 하지만 조건만 만족한다면 계수 정렬은 정렬해야 하는 데이터의 개수가 매우 많을때에도 효과적으로 사용 할 수 있다. 다만 일반적인 코딩 테스트의 시스템 환경에서는 메모리 공간상의 제약과 입출력 시간 문제로 인하여 입력되는 데이터의 개수를 1,000만 개 이상으로 설정할 수 없는 경우가 많기 때문에, 정렬 문제에서의 데이터 개수는 1,000만 개 미만으로 출제될 것이다. 계수 정렬의 공간 복잡도는 O(N+K) 이다.
본 포스팅은 ‘이것이 코딩 테스트다 with 파이썬’을 읽고 공부한 내용을 바탕으로 작성하였습니다.
작성자 : 엄코딩 eomcoding
'python' 카테고리의 다른 글
| Python 75 - 정렬 _ 실전 문제 1 ("위에서 아래로") (0) | 2021.07.06 |
|---|---|
| Python 74 - 정렬 _ 기준에 따라 데이터를 정렬 (정렬 라이브러리) (0) | 2021.07.05 |
| Python 72 - 정렬 _ 기준에 따라 데이터를 정렬 (퀵 정렬) (0) | 2021.07.03 |
| Python 71 - 정렬 _ 기준에 따라 데이터를 정렬 (삽입 정렬) (0) | 2021.07.02 |
| Python 70 - 정렬 _ 기준에 따라 데이터를 정렬 (선택 정렬) (0) | 2021.07.01 |